麻豆淫院

In recent years, topological materials have been studied extensively. A typical example of a topological material is a topological insulator, which is a unique insulator that does not conduct electricity inside the material, but allows electricity called spin current to flow on the surface.

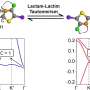
The difference between a normal insulator and a topological insulator can be mathematically expressed by the topological number. For example, a coffee cup with a handle can be transformed into a torus by continuous transformation, but it cannot be transformed into a shape without holes such as a ball or a cracker.

This is expressed as "topological difference," and the number of holes in this case corresponds to the topological number. There are other topological materials such as topological superconductors.

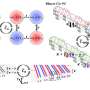
In a published in 麻豆淫院ical Review B, researchers proposed a new method to calculate the topological number for two-dimensional materials using the concepts of polarization theory and spiral boundary conditions.

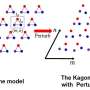
Polarization is a physical quantity that indicates the bias of the distribution of electrons in a material, and it is possible to know the information that appears on the surface when a sample is cut. The spiral boundary condition is a theoretical concept that encompasses two-dimensional lattice systems in one-dimensional order.

The study shows that the method of calculating topological numbers using polarization, which has been discussed so far in one-dimensional lattice systems, can be extended to two-dimensional systems.

This research is also theoretically significant in that it clarifies the correspondence with the method based on lattice gauge theory used in particle physics. The method can also be applied to the analysis of topological materials based on large-scale computer calculations.